《传感器原理与检测技术》课程知识速览

1 传感器基础理论※

1.1 定义与组成※

• 传感器的定义：

传感器概念的英语表述一般为：“A sensor is a device that receives a stimulus and responds with an electrical signal”。根据我国国家标准（GB/T 7665—2005），传感器（Transducer/Sensor）定义为：能感受被测量（Stimulus/Measurand）并按照一定的规律转换成可用输出信号的器件或装置，通常由敏感元件和转换元件组成。

• 传感器的组成：敏感元件、转换元件、测量电路。
  • 敏感元件：传感器中能直接感受（或响应）被测信息（非电量）的元件
  • 转换元件：传感器中能将敏感元件的感受（或响应）信号转换为电信号的部分

• 传感器的核心功能：物理量（非电量） → 电信号（电压、电流、频率等）

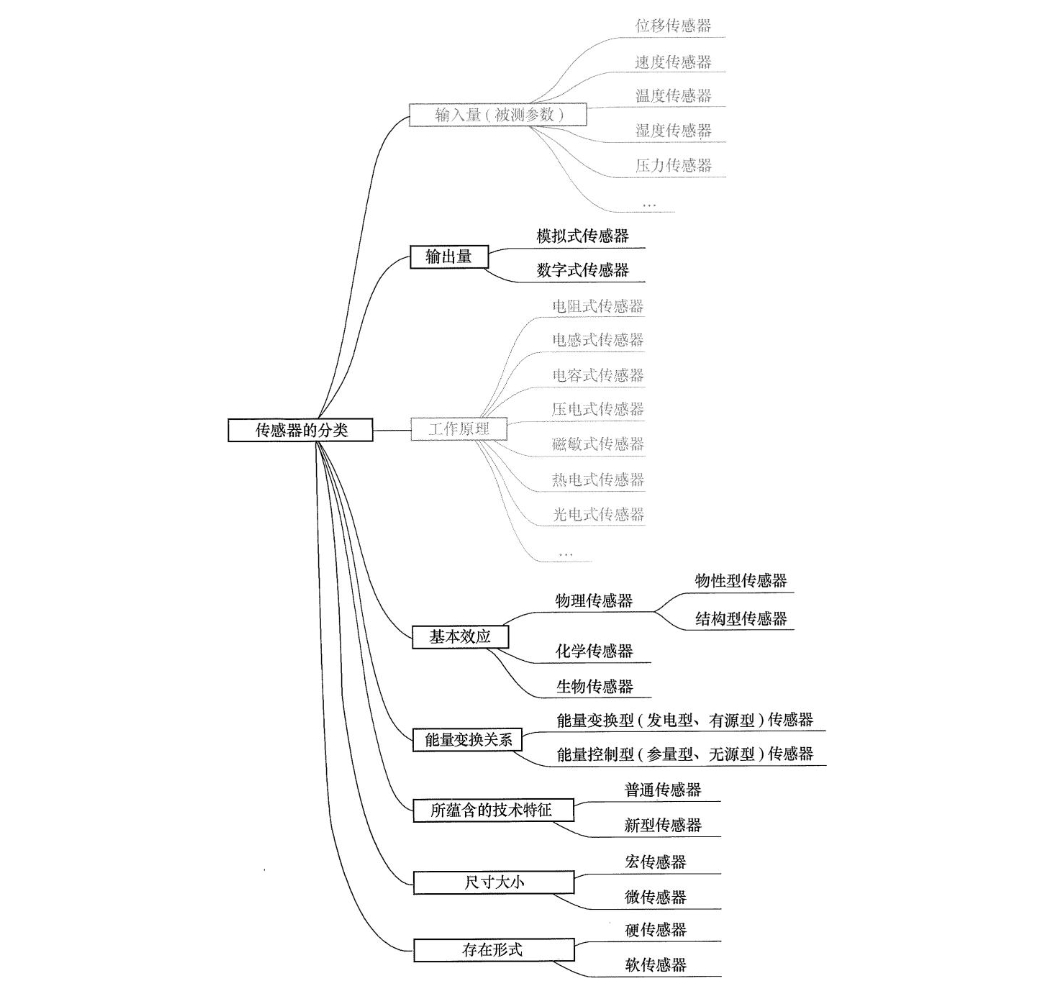
1.2 静态特性※

传感器的静态特性是它在稳态信号作用下的输入-输出关系。静态特性所描述的传感器的输入-输出关系式中不含时间变量。

衡量传感器静态特性的主要指标是线性度、灵敏度、分辨力、阈值、迟滞、重复性、漂移和精度。

1.2.1 线性度※

线性度（Linearity）是指传感器的输出与输入间成线性关系的程度。

1.2.2 灵敏度※

灵敏度（Sensitivity）是传感器在稳态下输出量变化对输入量变化的比值，通常用 \(S\) 或 \(K\) 来表示，即

对于线性传感器，它的灵敏度就是它的静态特性曲线的斜率；非线性传感器的灵敏度为一变量，即变化的斜率。

1.2.3 分辨力※

分辨力（Resolving Power）是指传感器能够感知或检测到的最小输入信号增量，反映传感器能够分辨被测量微小变化的能力。分辨力可以用能够分辨最小增量的绝对值或能够分辨最小增量与满量程的百分比来表示（此时称为分辨率，Resolution）。通常将模拟式传感器的分辨力规定为最小刻度分格值的一半，数字式传感器的分辨力是最后一位的一个字。灵敏度越高，分辨力越强（小）；反之亦然。

1.2.4 阈值※

阀值（Threshold Value）是能使传感器输出端产生可测变化量的最小被测输入量值，即零位附近的分辨力。大多数情况下，阈值主要取决于传感器的噪声大小。

1.2.5 迟滞※

迟滞（Hysteresis），也称回程误差，是在相同测量条件下，对应于同一大小的输入信号，传感器正（输入量由小增大）、反（输入量由大减小）行程的输出信号大小不相等的现象。

1.2.6 重复性※

重复性（Repeatability）表示传感器在输入量按同一方向做全量程（Span）多次测试时所得输入—输出特性曲线一致的程度，也称重复误差、再现误差。重复性表征传感器测量结果的分散性和随机性。实际特性曲线不重复的原因与迟滞产生的原因相同。

1.2.7 漂移※

漂移（Driftor Shift）是指传感器在输入量不变的情况下，输出量随时间或温度等变化的现象；漂移与被测输入量无关，将影响传感器的稳定性或可靠性（Stabilityor Reliability）。

产生漂移的原因主要有两个：一是传感器自身敏感材料特性和结构参数发生老化（即随时间缓慢变化), 称为时间漂移 (简称时漂), 分为零点漂移 (简称零漂, Zero Drift) 和灵敏度漂移 (Sensitivity Drift)。零点漂移是在规定条件下, 一个恒定的输入在规定时间内的输出在标称范围最低值处 (即零点) 的变化, 灵敏度漂移是指灵敏度随时间而产生的变化。二是在测试过程中周围环境 (如温度、湿度、压力等) 发生变化, 这种情况最常见的是温度漂移 (简称温漂), 它是由周围环境温度变化引起的输出变化。温度漂移通常用传感器工作环境温度偏离标准环境温度 (一般为  \(20^{\circ} \mathrm{C}\) ) 时输出值变化量与温度变化量之比来表示。

1.2.8 精度※

精度（Precision）也称静态误差，是传感器在满量程内任一点的测量输出值相对被测量理论值（真值）的偏离（或逼近）程度。

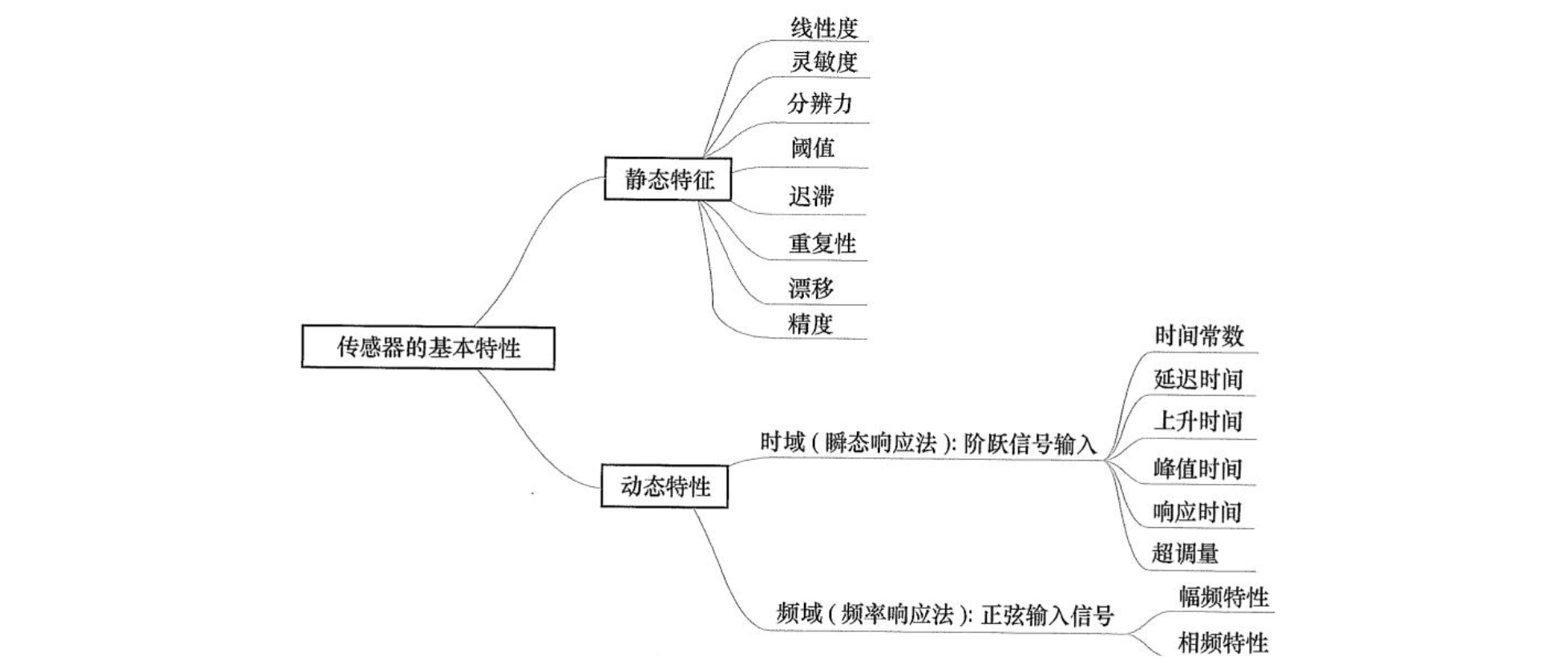
1.3 动态特性※

1.3.1 时域※

• 时间常数
• 延迟时间
• 上升时间
• 峰值时间
• 响应时间
• 超调量

1.3.2 频域※

• 幅频特性
• 相频特性

1.4 测量误差※

• 误差的概念
  • 真值：真值即实际值，是指在一定时间和空间条件下，被测物理量客观存在的实际值。
  • 误差：误差存在于一切测量中，误差(又称真误差) = 测量结果 - 被测量的真值。
  • 残余误差：残余误差(简称残差) = 测量结果 - 真值的最佳估计值(即约定真值)。
• 测量误差的分类
  • 随机误差：在测量中没有规律的单次扰动，多次测量可以表现出统计规律。
  • 系统误差：多次测量的误差不变或按一定规律变化，属于系统固有属性。
  • 粗大误差：测量结果中那些明显超出正常范围的误差，一般予以忽略，即认为测量无效。
• 误差的表示方法
  • \(\text{绝对误差} = \text{测得值} - \text{真值}\)
  • \(\text{相对误差} = \frac{\text{绝对误差}}{\text{被测真值}} \times 100\%\)

2 电阻式传感器※

电阻式传感器的基本工作原理是将被测量的变化转化为传感器电阻值的变化，再经一定的测量电路实现对测量结果的输出。

2.1 工作原理※

应变（Stress）是物体在外部压力或拉力作用下发生形变的现象。当外力去除后物体又能完全恢复其原来的尺寸和形状的应变称为弹性应变。具有弹性应变特性的物体称为弹性元件。应变效应是导体或半导体材料在力作用下产生机械变形、电阻值发生变化的现象。

应变电阻式传感器是利用电阻应变片将应变转换为电阻变化的传感器。应变电阻式传感器由弹性元件（作为敏感元件感知与力相关的量并产生应变）及在其上粘贴的电阻应变片（作为转换元件将应变转换为电阻变化）构成。应变电阻式传感器工作时引起的电阻值变化甚小，但其测量灵敏度较高。它在力、力矩、压力、加速度、重量等参数的测量中得到了广泛的应用。

应变电阻式传感器的基本工作原理：当被测物理量（如力、力矩或压力等）作用在弹性元件上使其发生形变，产生相应的应变，然后传递给与之相连的电阻应变片，引起电阻应变片的电阻值发生变化，通过测量电路变成电压等电量输出。输出的电压大小反映了被测物理量的大小。

2.1.1 应变效应※

通常把单位应变引起的电阻值相对变化量称为电阻丝的灵敏度系数，表示为：

由此可见，电阻丝的灵敏度系数受两个因素的影响：一个是受力后材料几何尺寸的变化，即  \((1 + 2\mu)\) ，对于确定的材料， \((1 + 2\mu)\)  是常数，其值约为  \(1 \sim 2\)  之间；另一个是受力后材料的电阻率的变化，即  \(\frac{\Delta\rho}{\rho\varepsilon}\) 。实验证明：在电阻丝拉伸极限内，电阻的相对变化与应变成正比，即  \(K\)  为常数。

2.1.2 电阻应变片种类※

在外力作用下，电阻应变片产生应变，导致其电阻值发生相应变化。应力（Strain）与应变的关系为

式中  

• \(\sigma\)  ——被测试件的应力；
• \(E\)  ——被测试件的材料弹性模量（弹性模量也叫杨氏模量，等同压强，单位为  \(\mathrm{Pa}\) ， \(1\mathrm{Pa} = 1\mathrm{N} / \mathrm{m}^2\) ）。

应力  \(\sigma\)  与力  \(F\)  和受力面积  \(A\)  的关系可表示为（是否也等同压强？）

常用的电阻应变片有两种：金属电阻应变片和半导体电阻应变片。

（1）金属电阻应变片（应变效应为主）

（2）半导体电阻应变片（压阻效应为主）

2.1.3 电阻应变片温度误差及其补偿※

1. 电阻应变片的温度误差（问题的提出）

电阻应变片敏感栅的电阻丝阻值随温度变化的关系可表示为

式中 

• \(R_{t}\)  ，  \(R_{0}\)  ——温度  \(t\)  和  \(0^{\circ}C\)  时的电阻值；
• \(\alpha_0\)  ——金属丝的电阻温度系数；
• \(\Delta t\)  ——变化的温度差值。

2. 电阻应变片温度误差补偿方法（问题的解决思路）

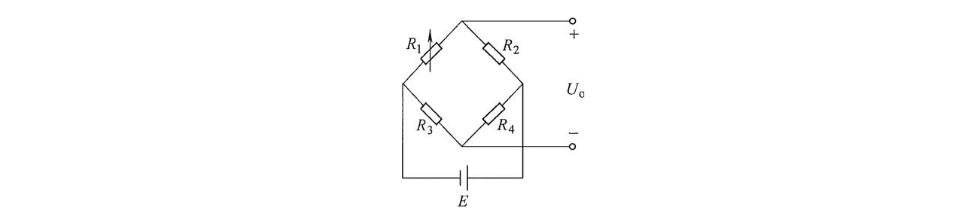
常用而有效的电阻应变片温度误差补偿方法是电桥补偿法，其电路图如下：

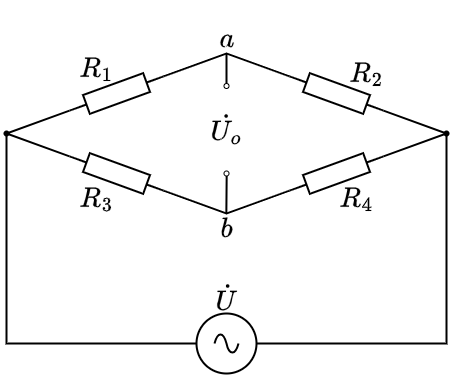
由电路图可知，电桥输出电压 \(\dot{U_o}\) 的计算公式如下：

测量方法：将工作电阻应变片  \(R_{1}\)  粘贴在被测试件表面上，补偿电阻应变片  \(R_{2}\)  粘贴在与被测试件材料完全相同的补偿块上，且只有工作电阻应变片承受应变，如图3-4b所示。这种单臂工作的测量电桥通常被称作惠斯通电桥（Wheatstone Bridge）。

（1）当被测试件不承受应变时

\(R_{1}\)  和  \(R_{2}\)  处于同一温度环境，通过调整电桥参数（即选取  \(R_{1} = R_{2} = R_{3} = R_{4}\) ）使之平衡，即

当温度变化（升高或降低）时，两个电阻应变片因温度引起的电阻变化量相同（ \(R_{1} = R_{2} = R_{3} = R_{4}\) ， \(\Delta R_{1} = \Delta R_{2}\) ），电桥仍处于平衡状态，即

（2）若被测试件有应变  \(\varepsilon\)  的作用

工作应变片电阻由应变引起的电阻增量  \(\Delta R_1' = R_1K\varepsilon\)  ，但补偿片不承受应变，不会有新的电阻增量。如果选取  \(R_{1} = R_{2} = R_{3} = R_{4}\)  ，一般有  \(\Delta R / R\ll 1\)  ，故此时电桥的输出电压为

由上式可知，在电阻丝灵敏度系数和电桥输入电压一定的条件下，电桥的输出电压 \(\dot{U}_o\) 只随被测试件的应变 \(\varepsilon\) 的变化而变化，与环境温度无关。

📌为了保证补偿效果，应注意以下几个问题：

1）在电阻应变片工作过程中，应保证 \(R_3 = R_4\)。

2）\(R_1\) 和 \(R_2\) 两个电阻应变片应具有相同的电阻温度系数 \(\alpha\)、线膨胀系数 \(\beta\)、应变灵敏度系数 \(K\) 和初始电阻值 \(R_0\)。

3）粘贴补偿片的材料和粘贴工作片的被测试件材料必须一样，两者线膨胀系数相同。

4）工作片和补偿片应处于同一温度场中。

例：如上图所示的应变片电桥测量电路，其中 \(R_1\) 为应变片，\(R_2\)、\(R_3\) 和 \(R_4\) 为普通精密电阻。应变片在0℃时电阻值为 \(100\Omega\)，\(R_2 = R_3 = R_4 = 100\Omega\)。已知应变片的灵敏度为 2.0，电源电压为 10V。
（1）如果将应变片 \(R_1\) 贴在弹性试件上，试件横截面积 \(A = 0.4 \times 10^{-4} m^2\)，弹性模量 \(E = 3 \times 10^{11} N/m^2\)，若受到 \(6 \times 10^4 N\) 拉力的作用，求测量电路的输出电压 \(U_o\)。
（2）在应变片不受力的情况下，假设该测量电路工作了 10min，且应变片 \(R_1\) 消耗的功率全转化为温升（设每焦耳能量导致应变片 0.1℃ 的温升），不考虑 \(R_2\)、\(R_3\) 和 \(R_4\) 的温升，应变片电阻温度特性为 \(R_t = R_0(1 + \alpha t)\)，\(\alpha = 4.28 \times 10^{-3} / ^\circ C\)。试求此时测量电桥的输出电压 \(U_o\)，并分析减小温度误差的方法。

解：

（1）根据题意，应力为 \(\sigma = F/A = 6 \times 10^4 / (0.4 \times 10^{-4}) N/m^2 = 1.5 \times 10^9 N/m^2\)

应变为 \(\varepsilon = \sigma / E = 1.5 \times 10^9 / (3 \times 10^{11}) = 0.005\)

应变导致的电阻变化 \(\Delta R = K \varepsilon R = 2.0 \times 0.005 \times 100 \Omega = 1 \Omega\)

因此，输出电压为

\[U_o = U_i \left( \frac{R_1 + \Delta R}{R_1 + \Delta R + R_2} - \frac{R_3}{R_3 + R_4} \right) = 10 \times \left( \frac{101}{201} - \frac{100}{200} \right) V = 0.0249 V\]

（2）根据题意，流过 \(R_1\) 的电流为 \(I = \frac{U_i}{R_1 + R_2} = \frac{10}{100 + 100} A = 0.05 A\)

则 \(R_1\) 上消耗的功率 \(P = I^2 R = 0.05^2 \times 100 W = 0.25 W\)

\(R_1\) 上消耗的能量 \(W = Pt = 0.25 \times 10 \times 60 J = 150 J\)

那么，温升 \(\Delta t = 150 \times 0.1 ^\circ C = 15 ^\circ C\)

此时，电阻 \(R_1\) 将变化为

\[R_1 = R_0 (1 + \alpha t) = 100 \times (1 + 4.28 \times 10^{-3} \times 15) \Omega = 106.42 \Omega\]

因此，对应的测量电桥输出电压如下：

方法一（无近似）

\[U_o = U_i \left( \frac{R_1}{R_1 + R_2} - \frac{R_3}{R_3 + R_4} \right) = 10 \times \left( \frac{106.42}{206.42} - \frac{100}{200} \right) V = 0.1555 V\]

方法二（利用单臂电桥输出电压的结论，有近似）

\[U_o \approx \frac{U_i}{4} \frac{\Delta R_1}{R_1} = \frac{U_i}{4} \frac{R_1 - R_0}{R_1} = \frac{10}{4} \times \frac{106.42 - 100}{106.42} V = 0.1508 V\]

值得指出的是，此时的  \(\Delta R_{t}\)  不是由被测力引起的，而是温度变化所引起的。由于此时应变片并未承受应变（追问：如果本例第2问的应变片同时受到第1问拉力的作用，测量电路的输出电压应为多少？），由此可见温度变化对测量结果的输出会带来较大的影响。要减小温度误差，可考虑采用的方法包括：不要长时间测量；对电阻  \(R_{1}\)  实施恒温措施；对电阻  \(R_{2}\)  做温度误差补偿，即采用补偿应变片。

本例第（2）问中，由于流过  \(R_{1}\)  的电流产生功耗，温度升高， \(R_{1}\)  的阻值是随温度升高而增加的，这将导致过程中流过  \(R_{1}\)  的电流、消耗的功率是变化的；本例在计算通过  \(R_{1}\)  的电流和  \(R_{1}\)  上消耗的功率与能量时并未计入  \(R_{1}\)  的变化，因此，得出的测量电桥的输出电压是。你觉得这样的质疑合理吗？

2.2 测量电路※

2.2.1 直流电桥※

（1）平衡条件

这就是电桥的平衡条件，即相邻两桥臂电阻的比值相等。

（2）电压灵敏度

为了测量电阻应变片的电阻微小变化，通常需加入放大器，放大器的输入阻抗比电桥输出阻抗大得多，因此可将电桥仍视为开路状态。当产生应变时，若电阻应变片电阻变化为  \(\Delta R_{1}\)  （工作电阻应变片为  \(R_{1}\) ），其他桥臂固定不变，则电桥平衡被打破，其输出电压  \(U_{\mathrm{o}} \neq 0\) ，即

设桥臂比为  \(R_{2} / R_{1} = n\)  ，由于  \(\Delta R_{1} <   <   R_{1}\)  ，因此分母中的  \(\Delta R_1 / R_1\)  可忽略，结合电桥平衡条件  \(R_{1} / R_{2} = R_{3} / R_{4}\)  ，可将式（3-30）简化为

定义电桥的电压灵敏度为

电压灵敏度越大，说明电阻应变片电阻相对变化相同的情况下，电桥输出电压越大，电桥越灵敏。

所以 \(n = 1\)（通常 \(R_1 = R_2 = R_3 = R_4\)）时，\(K_u\) 的值最大，电桥的电压灵敏度最高。此时有

（3）非线性误差及其补偿

式（3-31）是在略去分母中的较小量  \(\Delta R_{1} / R_{1}\)  得到的理想值，实际值应为

由于近似处理造成的非线性误差为

【注意】此非线性误差是来自上面公式推导过程中的近似等效导致的，实际值应为式 (3-36) ，因此只有使用了等效公式的前提下才有非线性误差，即在不采用差动电桥的情况下，非线性误差可以使用该公式进行计算，但是如果是差动电桥，则其非线性误差 \(\gamma_L = 0\) 

如果是四等臂电桥，即  \(R_{1} = R_{2} = R_{3} = R_{4}\)  ，  \(n = 1\)  ，则

例：如果将  \(120\Omega\)  的应变片贴在柱形弹性试件上，该试件的截面积  \(A = 0.5\times 10^{-4}\mathrm{m}^2\)  ，材料弹性模量  \(E = 2\times 10^{11}\mathrm{N / m}^2\)  。若由  \(5\times 10^{4}\mathrm{N}\)  的拉力引起应变片电阻变化为  \(1.2\Omega\)
（1）求该应变片的灵敏系数  \(K\)
（2）若将电阻应变片  \(R_{1}\)  置于单臂测量电桥, 电桥电源电压为直流  \(3 \mathrm{~V}\) , 求电桥输出的电压及其非线性误差 (设桥臂比为 1)。

解：

（1）应变片电阻的相对变化为

\[\frac {\Delta R}{R} = \frac {1 . 2}{1 2 0} = 0. 0 1\]

柱形弹性试件的应变为

\[\varepsilon = \frac {\sigma}{E} = \frac {F}{E A} = \frac {5 \times 1 0 ^ {4}}{2 \times 1 0 ^ {1 1} \times 0 . 5 \times 1 0 ^ {- 4}} = 0. 0 0 5\]

应变片的灵敏系数为

\[K = \frac {\Delta R / R}{\varepsilon} = \frac {0 . 0 1}{0 . 0 0 5} = 2\]

(2) 将电阻应变片  \(R_{1}\)  置于单臂测量电桥, 电桥电源电压为直流  \(3 \mathrm{~V}\) , 则电桥输出电压为

\[U _ {\mathrm {o}} = \frac {E}{4} \frac {\Delta R}{R} = \frac {3 \times 1 . 2}{4 \times 1 2 0} \mathrm {V} = 0. 0 0 7 5 \mathrm {V}\]

非线性误差为

\[\gamma_ {\mathrm {L}} = \frac {\Delta R / R}{1 + n + \Delta R / R} = \frac {0.01}{1 + 1 + 0.01} \approx 0.5 \%\]

要想减小或消除非线性误差，可采用的方法包括：

1. 提高桥臂比。
2. 采用差动电桥。差动电桥分半桥差动和全桥差动两种情形。

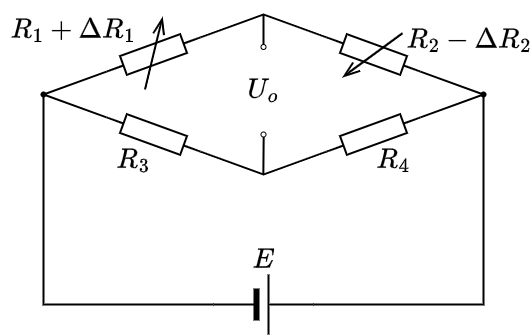
半桥差动如图所示，只有两个相邻桥臂接入电阻应变片。

该电桥的输出电压为

如果 \(\Delta R_1 = \Delta R_2, R_1 = R_2 = R_3 = R_4\)，则得到

可见，\(U_o\) 与 \(\Delta R_1\) 成线性关系，即半桥差动测量电路无非线性误差，且电桥电压灵敏度比单臂电阻应变片工作时提高了一倍。

若将电桥四臂都接入电阻应变片，如图所示，构成全桥差动测量电路

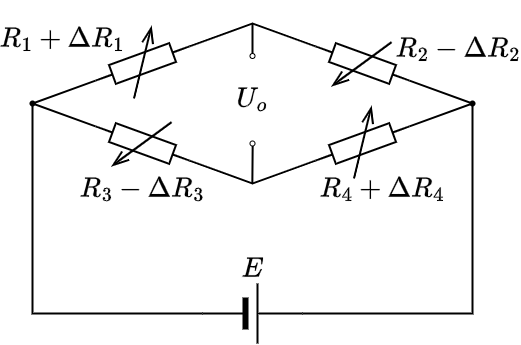
若 \(\Delta R_1 = \Delta R_2 = \Delta R_3 = \Delta R_4\)，且 \(R_1 = R_2 = R_3 = R_4\)，则

整理得到

可见，全桥差动测量电路不仅没有非线性误差，且电压灵敏度是单臂电阻应变片工作时的 4 倍。

例：某电阻应变片的电阻  \(R = 400\Omega\)  ，应变灵敏度系数  \(K = 2.05\)  设被测应变  \(\varepsilon = 1000\mu \mathrm{m / m}\)  。求：（1）  \(\Delta R / R\)  和  \(\Delta R\)  ；（2）如果电桥供电电源电压  \(E = 3V\)  ，计算全桥差动测量电路的输出电压。

解：

（1）根据电阻丝灵敏度系数计算公式，有

\[\frac {\Delta R}{R} = K \varepsilon = 2. 0 5 \times 1 0 0 0 \times 1 0 ^ {- 6} = 2. 0 5 \times 1 0 ^ {- 3}\]

相应地，  \(\Delta R = K\varepsilon R = 2.05\times 10^{-3}\times 400\Omega = 0.82\Omega\)

(2) 根据全桥差动测量电路, 有

\[U _ {\mathrm {o}} = E \frac {\Delta R}{R} = 3 \times 2. 0 5 \times 1 0 ^ {- 3} \mathrm {V} = 6. 1 5 \mathrm {m V}\]

2.3 典型应用※

例：在如图3-11所示的等强度梁式测力系统中，可能用到4个相同特性的电阻应变片 \(R_{1}\) 、 \(R_{2}\) 、 \(R_{3}\) 和 \(R_{4}\) ，各应变片灵敏度系数 \(K = 2\) ，初始电阻值为 \(100\Omega\) 。当试件受力 \(F\) 时，若应变片要承受应变，设其平均应变值 \(\varepsilon = 1000\mu \mathrm{m} / \mathrm{m}\) 。测量电路的直流电源电压为 \(3\mathrm{V}\) 。
（1）若只用一个电阻应变片构成单臂测量电桥，求电桥输出电压及电桥非线性误差。
（2）若要求用两个电阻应变片测量，且既要保持与单臂测量电桥相同的电压灵敏度，又要实现温度补偿，请画图标出两个应变片在悬臂梁上所贴的位置，绘出测量电桥。
（3）要使测量电桥电压灵敏度提高为单臂工作时的 4 倍, 请描述各个应变片在悬臂梁上应如何粘贴? 给出测量电桥, 并给出此时电桥的输出电压及电桥的非线性误差。

解：（1）设用电阻应变片  \(R_{1}\)  作测量电桥的测量臂，其他桥臂的初始电阻值为  \(100\Omega\)  。
由  \(\frac{\Delta R_1}{R_1} = K\varepsilon\)  可得

\[\frac {\Delta R _ {1}}{R _ {1}} = 2 \times 1 0 0 0 \mu = 2 \times 1 0 ^ {- 3}\]

设当  \(R_{1}\)  有  \(\Delta R_{1}\)  的变化时，电桥输出电压为  \(U_{\mathrm{ol}}\)

\[U _ {\mathrm {o l}} = \frac {E}{4} \frac {\Delta R _ {1}}{R _ {1}} = \frac {3}{4} \times 2 \times 1 0 ^ {- 3} \mathrm {V} = 1. 5 \times 1 0 ^ {- 3} \mathrm {V}\]

非线性误差：  \(\gamma_{\mathrm{L}} = \frac{\Delta R_{1} / R_{1}}{2 + \Delta R_{1} / R_{1}}\times 100\% \approx \frac{\Delta R_{1} / R_{1}}{2} = 0.1\%\)
（2）为了达到题设要求，应该在悬臂梁的正（反）面沿梁的长度方向贴测量应变片  \(R_{1}\) ，沿与梁的长度方向垂直的方向贴温度补偿应变片  \(R_{2}\) ，使得测量应变片和温度补偿应变片处于同一温度场中，如图所示。相应的测量电桥如图所示。

(3) 要使电桥电压灵敏度为单臂工作时的 4 倍, 则应该在悬臂梁的正、反面对应贴上 4 个相同的应变片: 两个接受拉力应变、两个接受压力应变，形成全桥差动电桥，如图所示。此时，电桥的输出电压为

\[U _ {\mathrm {o 2}} = E \frac {\Delta R _ {1}}{R _ {1}} = 0. 0 0 6 \mathrm {V}\]

电桥的非线性误差为

\[\gamma_ {\mathrm {L}} = 0\]

4 电感式传感器※

4.1 类型※

• 变磁阻电感式传感器（自感式）
  • 变磁阻电感式传感器由线圈、铁心和衔铁三部分组成。铁心和衔铁由导磁材料制成。
  • 为了减小非线性误差，实际测量中广泛采用差动变气隙电感式传感器。
• 电涡流电感式传感器（互感式）
  • 电涡流效应指的是这样一种现象：根据法拉第电磁感应定律，块状金属导体置于变化的磁场中或在磁场中作切割磁力线运动时，通过导体的磁通将发生变化，产生感应电动势，该电动势在导体表面形成电流并自行闭合，状似水中的涡流，称为电涡流。电涡流只集中在金属导体的表面，这一现象称为趋肤效应。

4.2 测量电路※

• 变磁阻电感式传感器（自感式）
  • 交流电桥式测量电路
  • 变压器式交流电桥
  • 谐振式测量电路
    • 谐振式调频式电路
    • 谐振式调幅式电路
• 电涡流电感式传感器（互感式）
  • 调频式电路
  • 调幅式电路

4.3 应用※

• 变磁阻电感式传感器（自感式）
  • 变气隙电感式压力传感器
• 电涡流电感式传感器（互感式）
  • 位移测量
  • 振幅测量
  • 转速测量
  • 无损探伤

5 电容式传感器※

电容式传感器利用了将非电量的变化转换为电容量的变化来实现对物理量的测量。电容式传感器具有结构简单、体积小、分辨率高、动态响应好、温度稳定性好、电容量小（一般为几十到几百微法）、负载能力差、易受外界干扰产生不稳定现象等特点。电容式传感器广泛用于位移、振动、角度、加速度，以及压力、差压、液面（料位或物位）、成分含量等的测量。

5.1 工作原理※

电容式传感器的常见结构包括平板状和圆筒状，简称平板电容器或圆筒电容器。

（1）平板电容器

在不考虑边缘效应的情况下，其电容量的计算公式为

式中

• \(A, d\) ——两平行板所覆盖的面积及之间的距离；
• \(\varepsilon, \varepsilon_r\) ——电容极板间介质的介电常数和相对介电常数；
• \(\varepsilon_0\) ——自由空间（真空）介电常数（根据国际单位制规定，\(\varepsilon_0 = \frac{10^{-9}}{36\pi}\text{F/m} \approx 8.85 \times 10^{-12}\text{F/m}\)）。

在实际使用中，通常保持其中两个参数不变，而只变其中一个参数，把该参数的变化转换成电容量的变化，通过测量电路转换为电量输出。因此，平板电容式传感器可分为三种：变极板覆盖面积的变面积型、变介质介电常数的变介质型和变极板间距离的变极距型。

（2）圆筒电容器

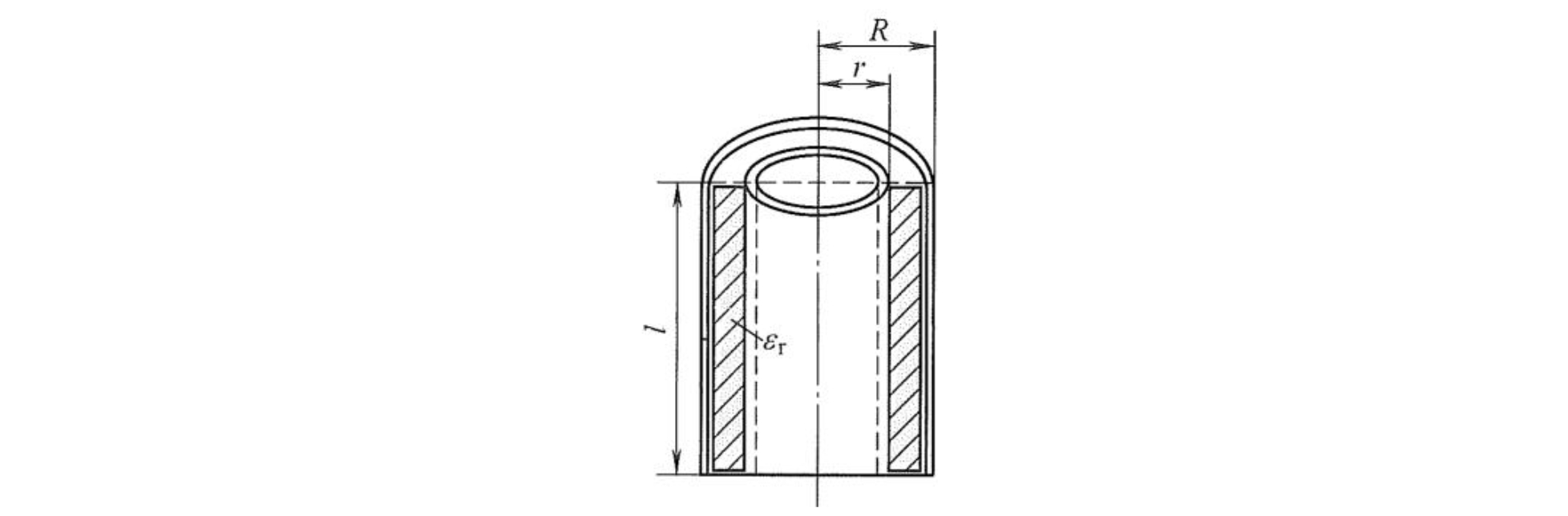
圆筒电容式传感器的结构如图所示。在不考虑边缘效应的情况下，其电容量的计算公式为

• 式中 \(l\) ——内外极板所覆盖的高度；
• \(R\)，\(r\) ——外极板的半径和内极板的半径。

5.1.1 圆筒结构※

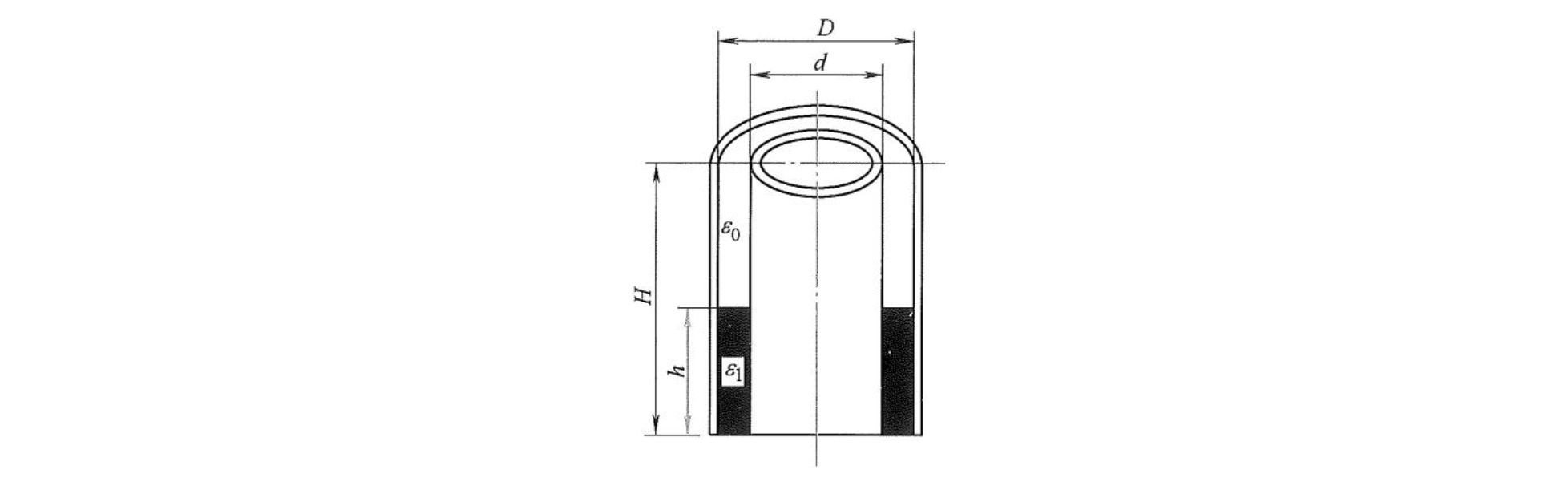
图为圆筒结构变介质型电容式传感器用于测量液位高低的结构原理图。设被测介质的相对介电常数为  \(\varepsilon_{1}\) ，液面高度为  \(h\) ，变换器总高度为  \(H\) ，内筒外径为  \(d\) ，外筒内径为  \(D\) ，此时相当于两个电容器的并联。对于筒式电容器，如果不考虑端部的边缘效应，它们的电容值分别为（近似认为空气的  \(\varepsilon_{\mathrm{r}} = 1\) ）

当未注入液体时的初始电容为

故总的电容值为（相当于两个电容器并联）

由式可见，电容改变量  \(\Delta C\)  与被测液位的高度  \(h\)  或介质的相对介电常数成线性关系。

由上总结可知：变介质型电容式传感器的电容改变量与输入量可能成线性关系，也可能成非线性关系，即：并联型平板结构和圆筒结构（相当于并联型）的电容改变量与介质的相对介电常数成线性关系，串联型平板结构的电容改变量与介质的介电常数成非线性关系。

• 采用差动结构的好处
  • 灵敏度得到一倍的改善
  • 线性度得到改善

5.2 测量电路※

• 调频电路
• 运算放大器
• 变压器式交流电桥
• 二极管双T型交流电桥
• 脉冲宽度调制电路

6 压电式传感器※

6.1 工作原理※

6.1.1 压电效应※

压电式传感器是以某些介质的压电效应作为工作基础的。所谓压电效应，就是对某些电介质沿一定方向施以外力使其变形时，其内部将产生极化而使其表面出现电荷集聚的现象，也称为正压电效应。不同于压阻效应只产生阻抗变化，压电效应会产生电荷。由于某些介质材料具有压电效应，在受力作用而变形时，在两个表面上产生符号相反的电荷，在外力去除后又重新恢复到不带电状态，使机械能转变为电能。

当在片状压电材料的两个电极面上加交流电压，那么压电片将产生机械振动，即压电片在电极方向上产生伸缩变形，压电材料的这种现象称为电致伸缩效应，也称为逆压电效应。逆压电效应是将电能转变为机械能。逆压电效应说明压电效应具有可逆性。

利用逆压电效应可以制成电激励的制动器（执行器）；基于正压电效应可制成机械能的敏感器（检测器），即压电式传感器。当有力作用于压电材料上时，传感器就有电荷（电压）输出。压电式传感器是典型的有源传感器。

压电式传感器的特点：结构简单、体积小、重量轻、工作频带宽、灵敏度高、信噪比高、工作可靠、测量范围广等。

压电式传感器的用途：主要用于与力相关的动态参数测试，如动态力、机械冲击、振动等，它可以把加速度、压力、位移、温度等许多非电量转换为电量。

6.1.2 压电材料※

• 石英晶体（单晶体）
• 压电陶瓷（多晶体）
• 压电高分子材料

6.2 测量电路※

1. 压电传感器到底是个什么东西？（等效电路）

• 初学者理解：
  • 你可以把压电传感器想象成一个“发电的海绵”。
    • 当你挤压它（受力）时，它会挤出“电荷”（就像海绵挤出水）。
    • 但它本身又是一个绝缘体，所以挤出来的电荷跑不掉，会聚集在表面。
• 课本原理翻译：
  • 为什么等效为电容？
    • 电容是用来储存电荷的容器。压电传感器有两个金属面，中间夹着绝缘的压电材料，这种结构在物理上就是典型的“电容器”结构。
  • 为什么有两种模型？
    • 这就好比我们可以把电池看作是“提供电压的源头”，也可以看作是“提供电流的源头”。
    • 电荷源模型：把它看作一个会产生电荷 \(Q\) 的发生器，和一个电容并联——电荷等效电路
    • 电压源模型：把它看作一个会产生电压 \(U\) 的电池，和一个电容串联——电压等效电路
    • 实际情况：现实中没有完美的绝缘体，电荷会慢慢漏掉，电路中也有电缆，所以实际电路中还要加上“泄漏电阻”（漏气孔）和“电缆电容”（额外的容器）。

2. 为什么要接一个“前置放大器”？（测量电路）

• 初学者理解：
  • 压电传感器产生的信号非常“娇气”（内阻极高，能量极小）。如果你直接拿一个普通万用表去测，信号瞬间就没了（因为普通表的内阻不够高，电荷瞬间就被吸干了）。
• 课本原理翻译：
  • 前置放大器有两个核心作用：
    • “保镖”作用（阻抗变换）：传感器的内阻抗高达 \(10^{10} \Omega\)（100亿欧姆）。放大器负责把这个极高的阻抗转换成低的输出阻抗，让后续的仪表能轻松读取信号，而不损失能量。
    • “大喇叭”作用（信号放大）：传感器出来的信号太微弱，需要放大才能用。

3. 两类放大器：为什么“电荷放大器”更受欢迎？

这是考试和应用中的核心考点。

• A. 电压放大器（简单的那个）
  • 原理：直接把传感器产生的电压放大。
  • 致命缺点：怕长电缆。
    • 为什么？ 电缆本身也是一种“电容”。在电压放大电路中，传感器、电缆、放大器三者的电容是并联在一起的。根据公式，电缆越长，总电容就越大，分到的电压就越小。
    • 后果：如果你换了一根长一点的导线，测量结果就变了，必须重新校准。这在工业上太麻烦了。
• B. 电荷放大器（好用的那个）
  • 原理：利用一个特殊的反馈电容，把电荷“锁”在放大器里。
  • 核心优势：无视电缆长度。
    • 为什么？ 它的输出电压只取决于“电荷量”和放大器自带的“反馈电容”，跟电缆电容几乎没关系。
    • 后果：无论你导线接多长，只要反馈电容不变，测量结果就是准的。这是它的突出优点。

4. 为什么压电传感器不能测“静态”力？

• 初学者理解：
  • 还记得前面的“海绵”比喻吗？
    • 动态（动次打次）：你不断地捏海绵、松海绵，水（电荷）就会不断地进进出出，形成水流（电流），仪表能测到。
    • 静态（死死捏住）：如果你用力捏住海绵不动。一开始会挤出水，但因为没有新的动作，而且周围有“漏孔”（泄漏电阻），水很快就流光或干掉了，最后仪表显示为0。
• 课本原理翻译：
  • 漏电是不可避免的：传感器和放大器都有电阻，不是绝对绝缘的。
  • 静态失效：当外力不变（静态）时，产生不了新的电荷。原有的电荷会通过电阻慢慢漏掉（放电）。只有当外力快速变化（动态）时，补充电荷的速度快过漏电的速度，才能测出信号。

5. 压电片为什么要“串联”或“并联”？

单个压电片产生的电太弱了，我们需要像叠罗汉一样把它们组合起来。

• A. 并联法（像并联电池）
  • 怎么接：正极接正极，负极接负极。
  • 效果：
    • 电荷量变大（两个水桶一起倒水，水量加倍）。
    • 电容量变大。
  • 用途：适合需要大电荷输出的场合，因为电荷多了，信号更有底气，适合测慢一点的信号。
• B. 串联法（像串联电池）
  • 怎么接：正极接负极（首尾相连）。
  • 效果：
    • 电压变大（两节电池串联，电压加倍）。
    • 电容量变小。
  • 用途：适合需要高电压输出的场合，或者像电压放大器这种自身输入阻抗很高的电路。

总结给初学者：

1. 压电传感器就像发电海绵，捏它才有电，不捏（或捏着不动）电就漏光了，所以只能测动态力。
2. 为了怕电漏光，必须接高阻抗的前置放大器。
3. 电荷放大器最好用，因为不怕导线长短变化。
4. 并联出大电荷，串联出大电压。

8 热电式传感器※

在工业生产过程中，温度通常是需要测量和控制的重要参数之一。热电式传感器是一种能将温度变化转换为电量变化的元件。在各种热电式传感器中，除有一类集成温度传感器直接将温度转换成电压或电流输出外（如LM135和DS18B20为电压输出、AD590为电流输出），以将温度转换为电动势或电阻的方法最为普遍，对应的元件分别称为热电偶、热电阻和热敏电阻。即热电偶是将温度变化转换为电动势变化的测温元件；热电阻和热敏电阻是将温度变化转换为电阻变化的测温元件。

8.1 热电偶※

8.1.1 热电效应※

如图所示，两种不同的导体两端相互紧密地连接在一起，组成一个闭合回路。当两接点温度不等时（设  \(t > t_0\) ），回路中就会产生大小和方向与导体材料及两接点的温度有关的电动势，从而形成电流，这种现象称为热电效应。

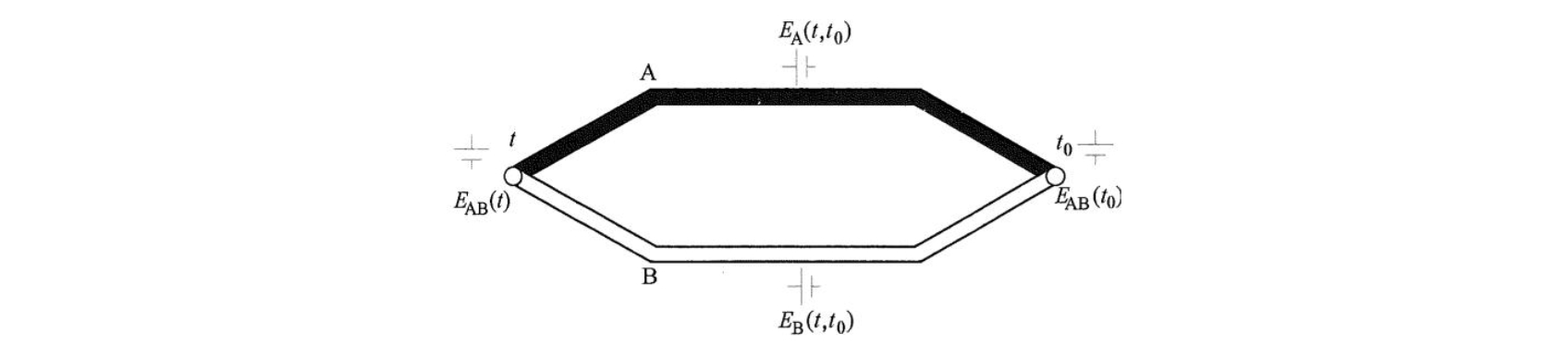
它是1821年T.J.Seebeck用铜和锑做实验时发现的，因此也称为塞贝克效应（Seebeck Effect）。该电动势称为热电动势；把这两种不同导体的组合称为热电偶，称A、B两导体为热电极。两个接点，一个为工作端或热端  \((t)\) ，测温时将它置于被测温度场中；另一个为自由端或冷端  \((t_0)\) ，一般要求它恒定在某一温度。

实际上，热电动势来源于两个方面，一部分由两种导体的接触电动势构成，另一部分是单一导体的温差电动势。

• 接触电动势（两种导体）：由于两种不同导体的自由电子密度不同而在接触处形成的电动势。
• 温差电动势（单一导体）：同一导体的两端因其温度不同而产生的一种电动势。

热电偶、热电势、热电极

热端（测量端或工作端）、冷端（参考端或自由端）

• 普通型热电偶
• 特殊热电偶
  • 铠装型热电偶
  • 薄膜热电偶

8.1.2 热电偶的基本定律※

1. 中间导体定律

• 课本定义：在热电偶测温回路中接入第三种导体（如导线、仪表），只要该导体两端的连接点温度相同，它就不会影响回路的总热电动势。
• 小白人话版（仪表接入法则）：
  • 是什么：这个定律告诉你，热电偶的回路里可以随便接各种仪表和导线。
  • 怎么理解：热电偶本身是个闭合回路，如果你想测量它的电压，必须把它剪开接个电压表进去。你可能会担心：“加了个电压表（第三种金属），会不会干扰原来的信号？”这个定律告诉你：只要接电压表的那两个接线柱温度一样，就完全没影响。
  • 用处：这是我们可以用万用表、毫伏表来测量热电偶信号的理论基础。

2. 中间温度定律

• 课本定义：热电偶在接点温度为 \(t\) 和 \(t_0\) 时的热电动势，等于它在 \((t, t_c)\) 和 \((t_c, t_0)\) 两段热电动势的代数和。公式为：\(E_{AB}(t, t_0) = E_{AB}(t, t_c) + E_{AB}(t_c, t_0)\)。
• 小白人话版（接力跑法则）：
  • 是什么：测量一段大的温差，可以拆成两段小的温差相加。
  • 怎么理解：假设你要测 1000℃ 到 0℃ 的电压，你可以先测 1000℃ 到 20℃ 的电压，再测 20℃ 到 0℃ 的电压，把两个加起来，结果是一样的。
  • 用处：这是“补偿导线”存在的依据。因为热电偶贵金属（如铂）很贵，我们可以用便宜的导线（在低温段特性和贵金属一样）把信号“接力”延长到仪表处，既省钱又准确。

3. 标准电极定律

• 课本定义：如果导体 A 和 B 分别与第三种导体 C（标准电极）组成热电偶的热电动势已知，那么 A 和 B 组成的热电偶的热电动势也可以计算出来。公式为：\(E_{AB} = E_{AC} - E_{BC}\)。
• 小白人话版（参照物法则）：
  • 是什么：不需要把世界上所有金属两两组合去测试，只要大家都和一个“标准”比就行了。
  • 怎么理解：假设你要知道小明和小红的身高差（\(A-B\)），但你没有直接量他们的尺子。你可以找一个“标准人”小刚（\(C\)）。量出“小明比小刚高多少”（\(A-C\)），再量出“小红比小刚高多少”（\(B-C\)），两个一减，就算出小明和小红的差值了。通常这个“标准人”是高纯度铂。
  • 用处：大大简化了数据表。我们只需要测各种金属对“铂”的数据，其他任意两种金属组合的数据都可以算出来。

例：热端为 100℃ ，冷端为 0℃ 时，镍铬合金与纯铂组成的热电偶的热电动势为 \(2.95mV\) ，而考铜与纯铂组成的热电偶的热电动势为 \(-4.0mV\) ，则镍铬合金和考铜组成的热电偶所产生的热电动势应为：\(E_{AB}(t,t_0) = E_{AC}(t,t_0) - E_{BC}(t,t_0) = 2.95mV - (-0.4mV) = 6.95mV\)

4. 均质导体定律

• 课本定义：如果组成热电偶的两个热电极材料相同，无论两端温度怎么变化，回路的总热电动势永远为 0。
• 小白人话版（双胞胎无效法则）：
  • 是什么：做热电偶必须用两种不一样的金属。
  • 怎么理解：热电偶发电靠的是两种不同金属对电子的吸引力不同。如果你拿两根一模一样的铁丝拧在一起，加热一端，电子在两根铁丝里跑得一样快，互相抵消，发不出电来。
  • 用处：用来检查材料纯不纯。如果你把一根丝的两头接起来加热，居然有电，说明这根丝材料不均匀（不仅质）。

8.1.3 热电偶的冷端温度补偿※

• 为什么要进行冷端补偿?
  • 因为热电势取决于两端温度差，冷端需恒定或补偿。
• 补偿导线的作用
  • 将冷端延伸到温度稳定的地方。

由热电偶的测温原理可以知道，热电偶产生的热电动势大小与两端温度有关，热电偶的输出电动势只有在冷端温度不变的条件下，才与工作端温度成单值函数关系。实际应用时，由于热电偶冷端离工作端很近，且又处于大气中，其温度受到测量对象和周围环境温度波动的影响，因而冷端温度难以保持恒定，这样会带来测量误差。进行冷端温度补偿的方法有以下四种。

（1）补偿导线法

热电偶的长度一般只有  \(1\mathrm{m}\)  左右，要保证热电偶的冷端温度不变，可以把热电极加长，使自由端远离工作端，放置到恒温或温度波动较小的地方，但这种方法对于由贵金属材料制成的热电偶来说将使投资增加，解决的办法是采用一种称为补偿导线的特殊导线，将热电偶的冷端延伸出来，如图所示。补偿导线实际上是一对与热电极化学成分不同的导线，在  \(0\sim 150^{\circ}\mathrm{C}\)  温度范围内与配接的热电偶具有相同的热电特性，但价格相对便宜。利用补偿导线将热电偶的冷端延伸到温度恒定的场所（如仪表室），且它们具有一致的热电特性，相当于将热电极延长，根据中间温度定律，只要热电偶和补偿导线的两个接触点温度一致，就不会影响热电动势的输出。常用热电偶补偿导线类型见表8-7，根据表中数据可知，补偿导线主要用于贵金属制成的热电偶的补偿，对于非贵金属通常用制作热电极的材料本身进行补偿。

（2）冷端恒温法

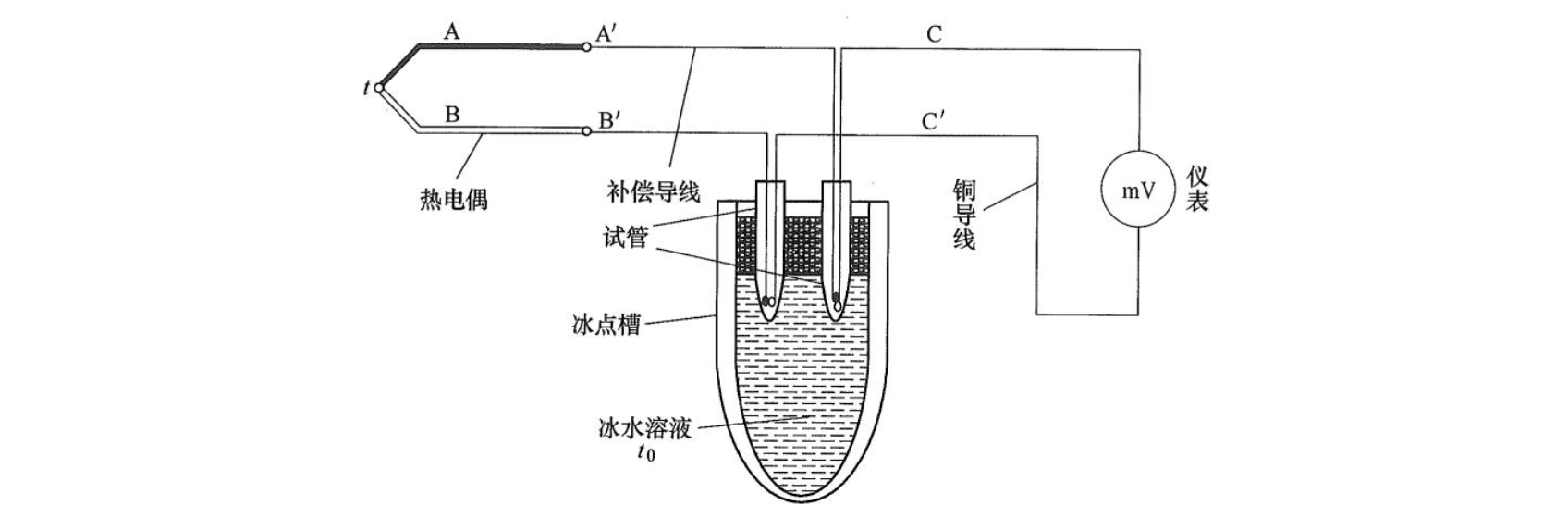
冷端恒温法就是把热电偶的冷端置于某些温度不变的装置中，以保证冷端温度不受热端测量温度的影响。恒温装置可以是电热恒温器或冰点槽（槽中装冰水混合物，温度保持在  \(0^{\circ}\mathrm{C}\) ），前者的温度不为  \(0^{\circ}\mathrm{C}\) ，还需要对热电偶进行冷端温度校正；后者为了避免冰水导电引起两个连接点短路，必须把连接点分别置于两个玻璃试管里，浸入同一冰点槽，使之相互绝缘，如图所示。这种方法仅限于在科学实验中使用。

（3）冷端温度校正法

如果热电偶的冷端温度偏离  \(0^{\circ}\mathrm{C}\) ，但稳定在温度  \(t_0\) ，则按式\(E _ {\mathrm {A B}} (t, t _ {0}) = E _ {\mathrm {A B}} (t, t _ {\mathrm {c}}) + E _ {\mathrm {A B}} (t _ {\mathrm {c}}, t _ {0})\)（即中间温度定律）对仪表指示值进行修正，即

式中 

• \(t\)  ——工作端温度；
• \(t_0\)  ——冷端的实际温度；
• 0——冷端的标准温度（ \(0^{\circ}\mathrm{C}\) ，便于查表）；
• \(E(t, t_0)\)  ——热电偶工作在  \(t\)  与  \(t_0\)  时，仪表测出的热电动势值；
• \(E(t,0), E(t_0,0)\)  ——冷端温度为  \(0^{\circ}\mathrm{C}\) ，工作端温度为  \(t\)  和  \(t_0\)  时的热电动势值（由热电偶分度表中查得）。

（4）自动补偿法

自动补偿法也称电桥补偿法，它是在热电偶与仪表间加上一个补偿电桥，当热电偶冷端温度升高，导致回路总电动势降低时，这个电桥感受自由端温度的变化，产生一个电位差，其数值刚好与热电偶降低的电动势相同，两者互相补偿。这样，测量仪表上所测得的电动势将不随自由端温度而变化。自动补偿法解决了冷端温度校正法不适合连续测温的问题。

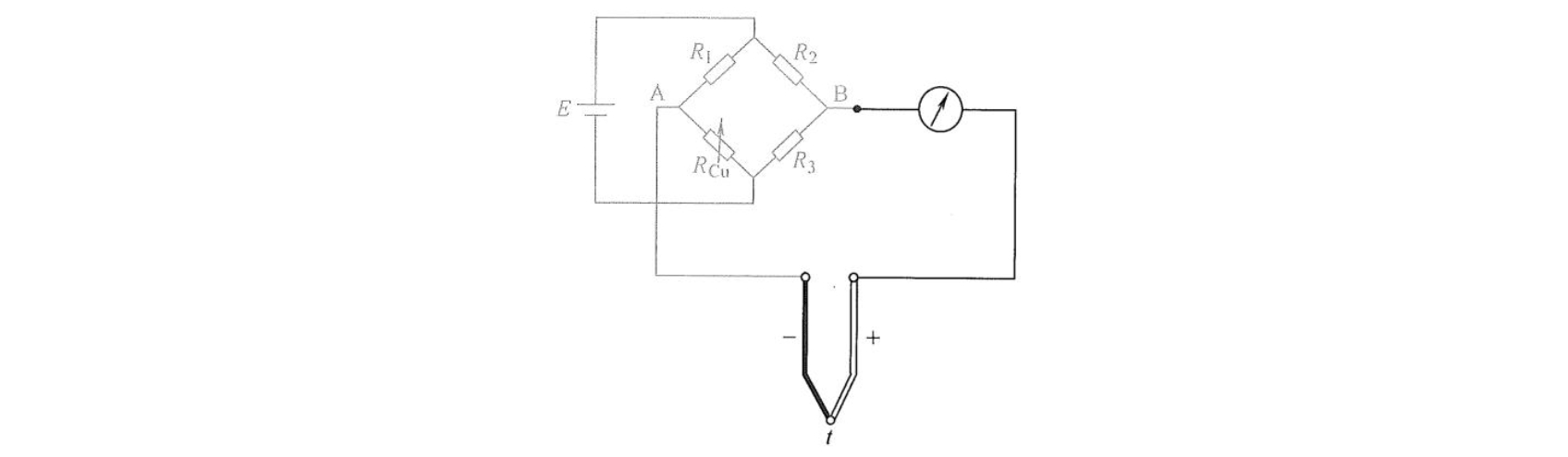
如图所示，补偿电桥是一个直流不平衡电桥，它由三个电阻温度系数较小的锰铜丝绕制的电阻 \(R_{1}\) 、 \(R_{2}\) 、 \(R_{3}\) 和电阻温度系数较大的铜丝绕制的电阻 \(R_{\mathrm{Cu}}\) 和稳压电源组成。补偿电桥与热电偶参考端处在同一环境温度，设计时使电桥在  \(20^{\circ}\mathrm{C}\) （或  \(0^{\circ}\mathrm{C}\) ）处于平衡状态，此时电桥的A、B两端无电压输出，电桥对仪表无影响。当环境温度变化时，热电偶冷端温度随之变化，这将导致热电动势发生改变，但此时  \(R_{\mathrm{Cu}}\)  的阻值也随温度变化而变化，电桥平衡被破坏，电桥A、B 两端将有不平衡电压输出, 不平衡电压与热电偶的热电动势叠加在一起输入测量仪表。如果适当选择桥臂电阻和桥路电流, 就可以使电桥产生的不平衡电压  \(U_{\mathrm{AB}}\)  正好补偿由于参考端温度变化引起的热电动势  \(E_{\mathrm{AB}}(t, t_{0})\)  的变化量, 从而达到自动补偿的目的。补偿目标为

电桥不平衡输出电压为

式中  \(E\)  ——加在电桥上的电压。

8.2 热电阻※

热电阻作为一种感温元件，它是利用导体的电阻值随温度变化而变化的特性来实现对温度的测量。几乎所有的物质都具有这一特性，但作为测温用的热电阻一般要求：

• 电阻值与温度变化具有良好的线性关系。
• 电阻温度系数大，以便对温度变化敏感，便于精确测量。
• 电阻率高，热容量小，从而具有较快的响应速度。
• 在测量范围内具有稳定的物理、化学性质。
• 容易加工，价格尽量便宜。

根据以上要求，最常用的材料是铂和铜。工业上被广泛用来测量中低温区（ \(-200 \sim 850^{\circ}\mathrm{C}\) ）的温度。

热电阻由电阻体、保护套管和接线盒等部件组成，如图 a 所示。热电阻丝是绕在骨架上的，骨架采用石英、云母、陶瓷或塑料等材料制成，可根据需要将骨架制成不同的外形。为了防止电阻体出现电感，热电阻丝通常采用双线并绕法，如图 b 所示。

• 电阻丝采用双线并绕法（为什么？）
  • 为了防止电阻体出现电感

8.2.3 热电阻的测量电路※

1. 两线制（用于引线不长的短距离测量，精度较低）

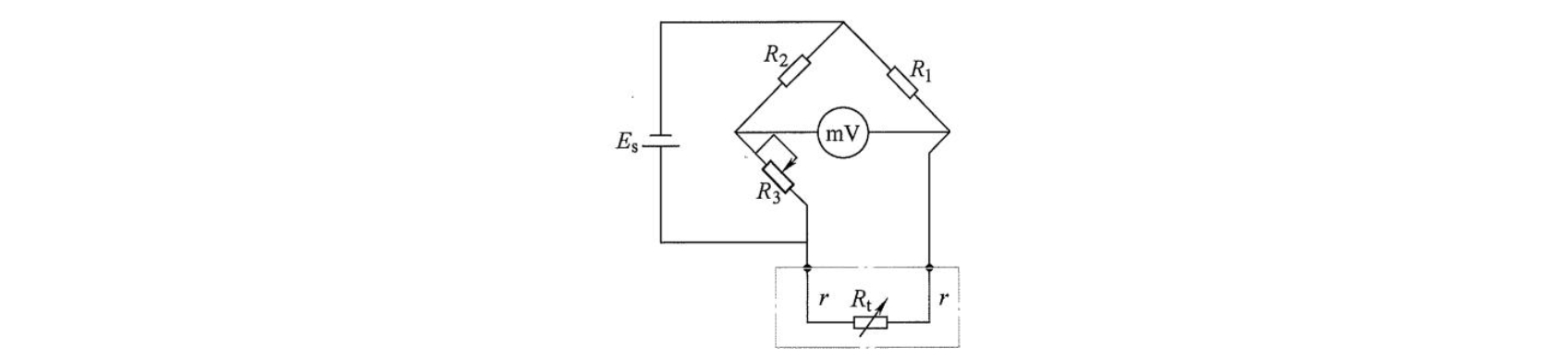
两线制的接线方式如图所示，在热电阻感温体的两端各连一根导线。设每根导线的电阻值为  \(r\) ，则电桥平衡条件为

因此有

这种引线方式简单、费用低，但是引线电阻以及引线电阻的变化会改变热电阻桥臂的总阻值，从而带来附加误差，因此，两线制适用于引线不长、测温精度要求较低，且引线电阻值远小于热电阻值的场合。

2. 三线制（用于较长距离的工业测量，一般精度）

由于热电阻的阻值很小，因此导线的电阻值不能忽视。如  \(R_{0} = 100\Omega\)  的铂电阻，  \(1\Omega\)  的导线电阻可能产生  \(3\%\)  左右的误差。为解决导线电阻的影响，工业热电阻大多采用三线制电桥连接法，如图8-21所示。图中  \(R_{t}\)  为热电阻，其三根引出导线相同，阻值都是  \(r\)  。其中一根与电桥电源相串联，它对电桥的平衡没有影响；另外两根分别与电桥的相邻两臂串联，当电桥平衡时，可得下列关系

所以有

如果使  \(R_{1} = R_{2}\) ，则式（8-40）就和  \(r = 0\)  时的电桥平衡公式完全相同，即说明此种接法导线电阻  \(r\)  对热电阻的测量毫无影响。注意：以上结论只有在  \(R_{1} = R_{2}\) ，且只有在平衡状态下才成立。为了消除从热电阻感温体到接线端子间的导线对测量结果的影响，一般要求从热电阻感温体的根部引出导线，且要求引出线一致，以保证它们的电阻值相等。

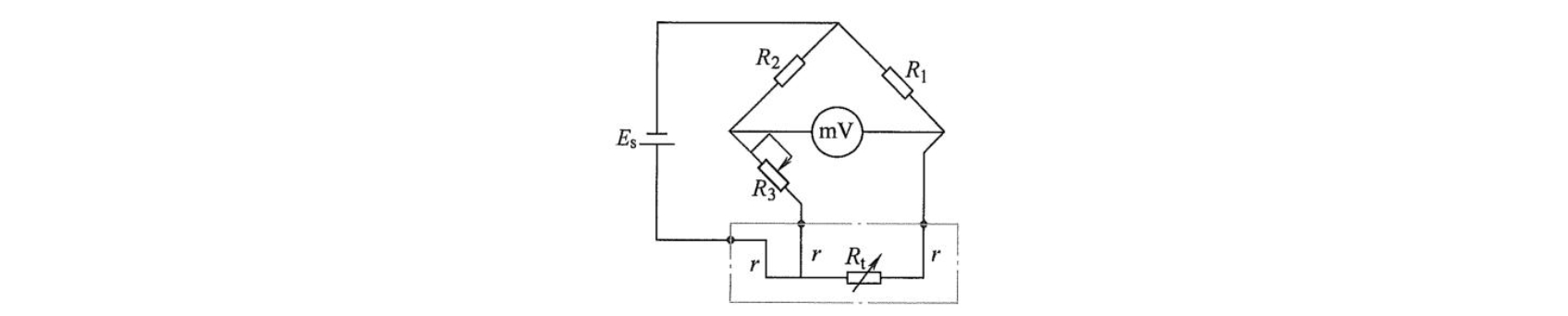
例：对于标号为  \(\mathrm{Pt}_{100}\)  的铂热电阻，如果采用两线制接法测温，设电桥电源为 \(10\mathrm{V},R_{1} = R_{2} = 1000\Omega ,R_{3} = 100\Omega\)  ，引线电阻  \(r = 5\Omega\)  ，如果被测温度为  \(300\%\)  ，试求两线制接法引起的相对测量误差。

解：

当  \(t = 300\%\)  时，铂热电阻的阻值为

\[\begin{array}{l} R _ {\mathrm {t}} = R _ {0} (1 + A t + B t ^ {2}) \\ = 1 0 0 (1 + 3. 9 1 \times 1 0 ^ {- 3} \times 3 0 0 - 5. 7 8 \times 1 0 ^ {- 7} \times 3 0 0 ^ {2}) \Omega \\ = 2 1 2. 1 \Omega \\ \end{array}\]

按三线制接法，引线电阻不会引起误差，其输出电压为

\[\begin{array}{l} U _ {0 1} = \left(\frac {R _ {\mathrm {t}} + r}{R _ {1} + R _ {\mathrm {t}} + r} - \frac {R _ {3} + r}{R _ {2} + R _ {3} + r}\right) E _ {\mathrm {s}} \\ = \left(\frac {2 1 2 . 1 + 5}{1 0 0 0 + 2 1 2 . 1 + 5} - \frac {1 0 0 + 5}{1 0 0 0 + 1 0 0 + 5}\right) \times 1 0 \mathrm {V} \approx 8 3 3. 5 \mathrm {m V} \\ \end{array}\]

按两线制接法，输出电压为

\[\begin{array}{l} U _ {0 2} = \left(\frac {R _ {\mathrm {t}} + 2 r}{R _ {1} + R _ {\mathrm {t}} + 2 r} - \frac {R _ {3}}{R _ {2} + R _ {3}}\right) \times E _ {\mathrm {s}} \\ = \left(\frac {2 1 2 . 1 + 2 \times 5}{1 0 0 0 + 2 1 2 . 1 + 2 \times 5} - \frac {1 0 0}{1 0 0 0 + 1 0 0}\right) \times 1 0 \mathrm {V} \approx 9 0 8. 3 \mathrm {m V} \\ \end{array}\]

因此，两线制接法引起的测量相对误差为

\[\gamma = \frac{U_{02} - U_{01}}{U_{01}}\times 100\% = \frac{908.3 - 833.5}{833.5}\times 100\% \approx 9\%\]

由上述计算结果可见，两线制接法引起的测量误差是存在的，有时还相当大，在实际测量中应高度重视。

3. 四线制（实验室用，高精度测量）

三线制接法是工业测量中广泛采用的方法。在高精度测量中，可设计成四线制的测量电路，如图所示。

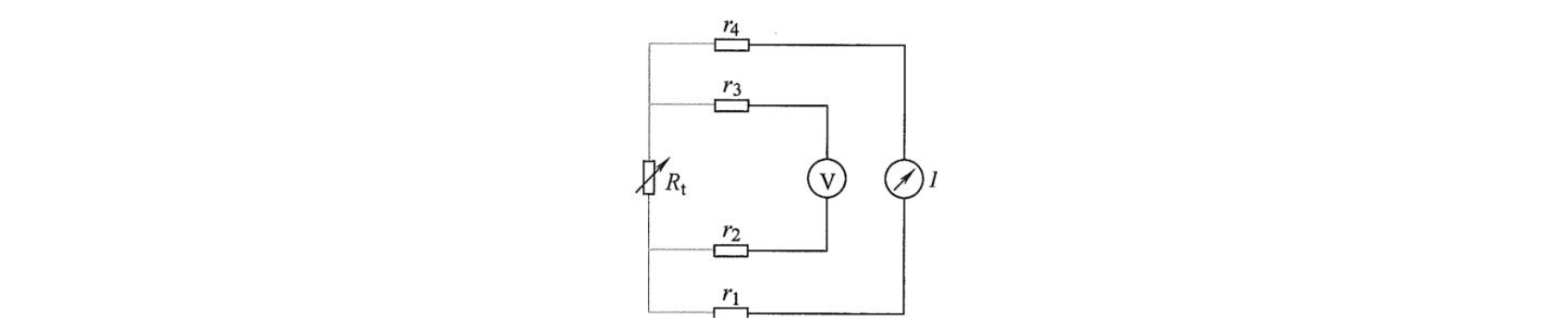
图中  \(I\)  为恒流源，测量仪表 V 一般用直流电位差计，热电阻上引出电阻值各为  \(r_{1} , r_{4}\)  和  \(r_{2} , r_{3}\)  的四根导线，分别接在电流和电压回路，电流导线上  \(r_{1} , r_{4}\)  引起的电压降不在测量范围内，而电压导线上虽有电阻但无电流（电位差计测量时不取用电流，认为内阻无穷大），所以四根导线的电阻对测量都没有影响。

热电阻的阻值可由测得的电压和恒流源的电流求出，即

8.3 热敏电阻※

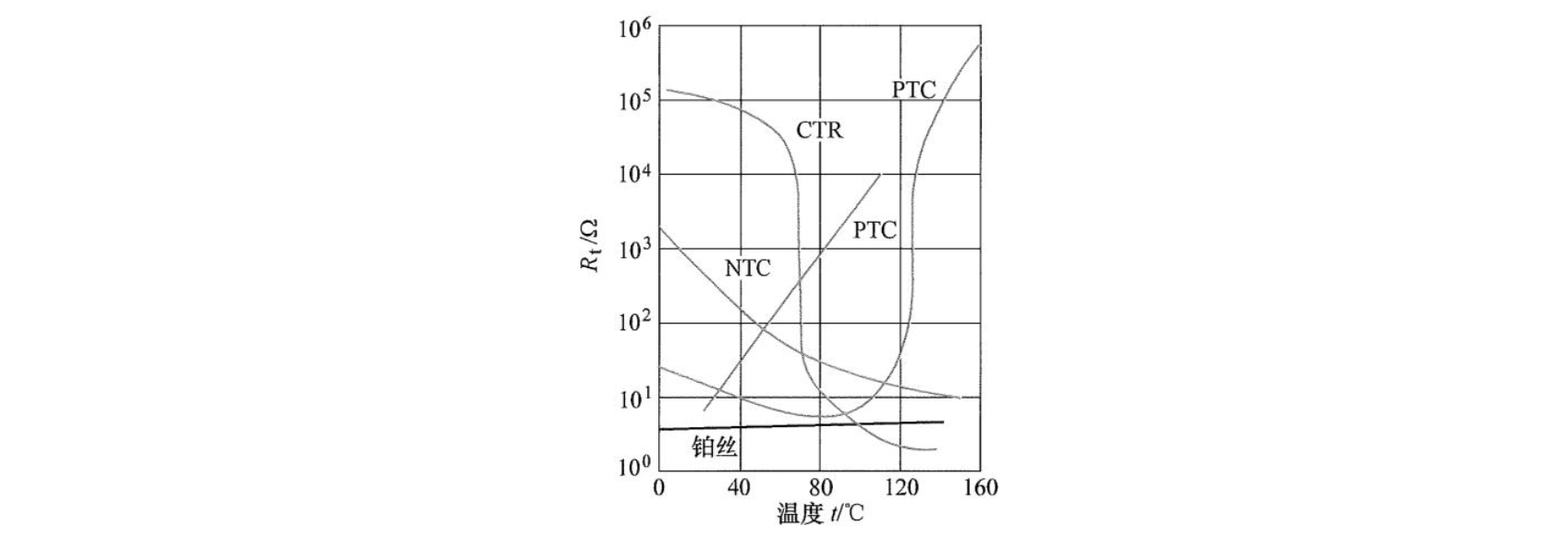
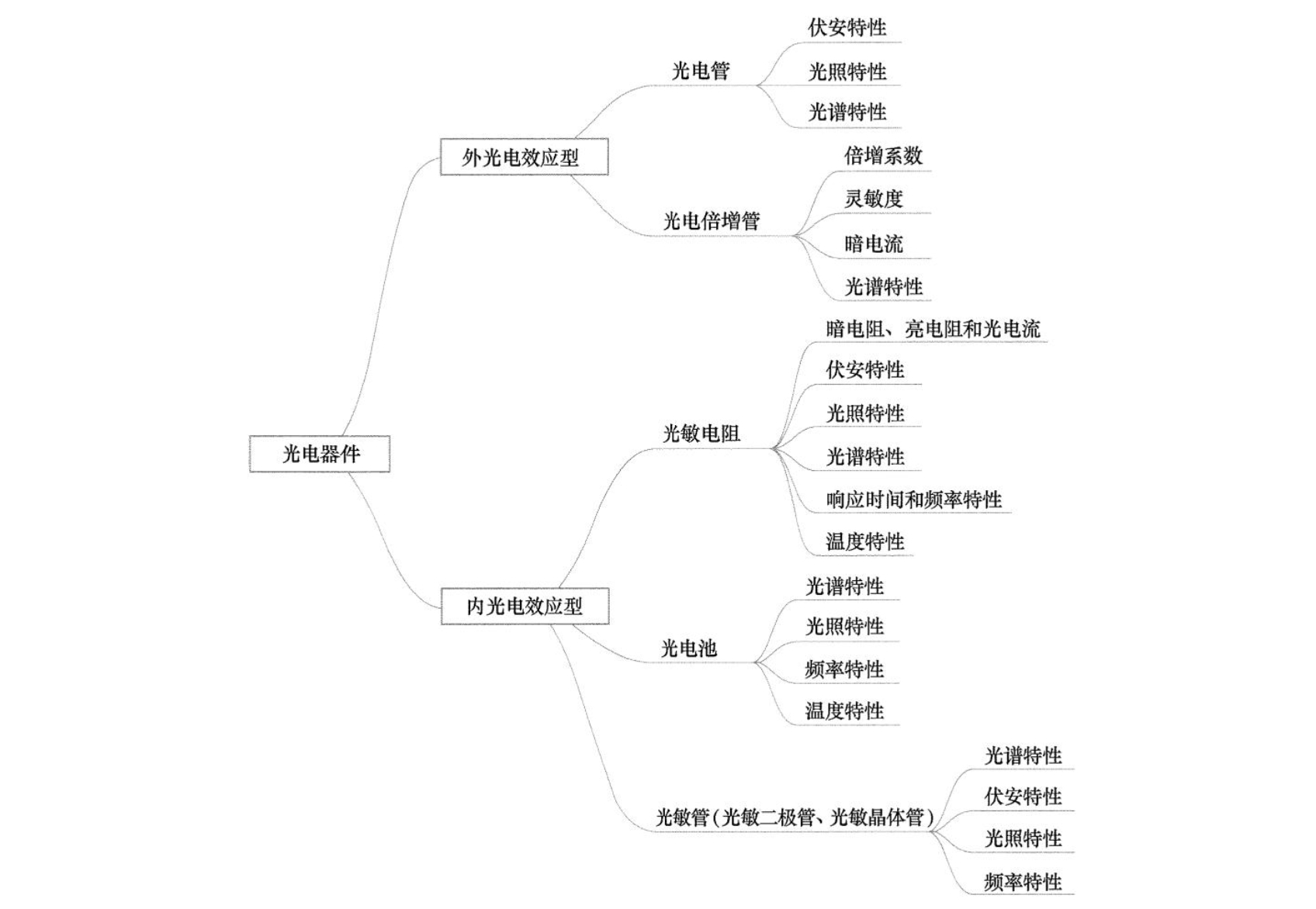
根据半导体的电阻-温度特性，热敏电阻可分为三类，即负温度系数（Negative Temperature Coefficient，NTC）热敏电阻、正温度系数（Positive Temperature Coefficient，PTC）热敏电阻和临界温度系数热敏电阻（Critical Temperature Resistors，CTR）。它们的温度特性曲线如图所示。

9 光电式传感器※

光电式传感器（或称光敏传感器）是利用光电器件把光信号转换成电信号或电参数（电压、电流、电荷、电阻等）的装置。光电式传感器工作时，先将被测量转换为光量的变化，然后通过光电器件把光量的变化转换为相应的电量变化，从而实现对非电量的测量。

光电式传感器具有结构简单、响应速度快、高精度、高分辨率、高可靠性、抗干扰能力强（不受电磁辐射影响，本身也不辐射电磁波）、可实现非接触式测量等特点，可以直接检测光信号，还可以间接测量温度、压力、位移、速度、加速度等，虽然它是发展较晚的一类传感器，但其发展速度快、应用范围广，具有很大的应用潜力。

• 按工作原理分类：
  • 光电效应传感器
  • 红外热释电探测器
  • 固体图像传感器
  • 光纤传感器

9.1 光电式传感器的基本形式※

光电式传感器可用来测量光学量或已转换为光学量的其他被测量，输出电信号。测量光学量时，光电器件作为敏感元件使用；测量其他物理量时，它作为转换元件使用。

光电式传感器由光路及电路两大部分组成。光路实现被测信号对光学量的调制；电路完成从光信号到电信号的转换。按测量光路组成来看，光电式传感器可分为四种基本形式：

（1）透射式光电传感器

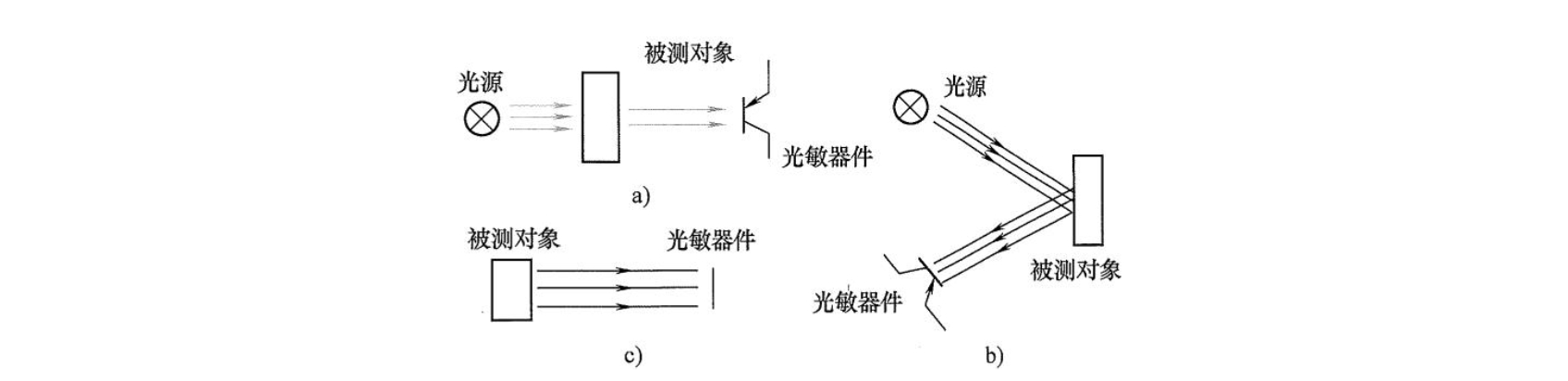
透射式光电传感器是利用光源发出一恒定光通量  \(\phi\) （luminous flux，是指人眼所能感觉到的光信号辐射功率，单位：流明，lm，相当于电学单位瓦特）的光，并使之穿过被测对象，其中部分光被吸收，而其余的光则到达光敏器件上，转变为电信号输出。如图 a 所示，根据被测对象吸收光通量的多少就可确定出被测对象的特性，此时，光敏器件上输出的光电流是被测对象所吸收光通量的函数。这类传感器可用来测量液体、气体和固体的透明度和浑浊度等参数。

（2）反射式光电传感器

反射式光电传感器是将恒定光源发出的光投射到被测对象上，由光敏器件接收其反射光通量，如图 b 所示。反射光通量的变化反映出被测对象的特性。例如：光通量变化大小可以反映出被测物体的表面光洁度；通过光通量的变化频率，可以反映出被测物体的转速。

（3）辐射式光电传感器

这种形式的传感器其光源本身就是被测对象，即被测对象是一辐射源。光电器件接收辐射能的强弱变化，如图 c 所示，光通量的强弱与被测参量（如温度）的高低有关。

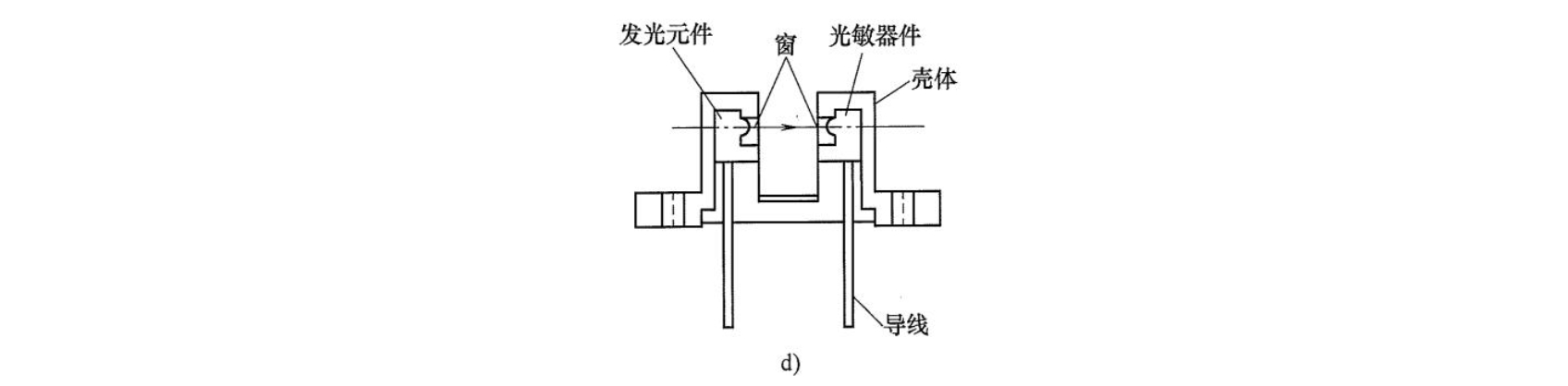
（4）开关式光电传感器

在开关式光电传感器的光源与光电器件间的光路上有物体时，光路被切断，否则，光路畅通，如图 d 所示。光敏器件上表现出有光（无物体阻挡）就有电信号，无光（有物体阻挡）则无电信号，即仅为“0”或“1”的两种开关状态。它的使用形式有开关、计数和编码三种，如点钞机用两组红外发光二极管和光敏晶体管实现纸币完整性检测和计数。

完成光电检测需要设计一定形式的光路图，光路由光学元件组成。光学元件有透镜、滤光片、光阑、光楔、棱镜、反射镜、光通量调制器、光栅及光导纤维等。通过它们实现光参数的选择、调制和处理。在测量其他物理量时，还需配以光源和调制件。常用的光源有白炽灯、发光二极管和半导体激光器等，用以提供恒定的光照条件；调制件是用来将光源提供的光量转换成能与被测量对应变化的光量的器件，调制件的结构依被测量及测量原理而定。

常用的光电转换元器件有真空光电管、充气光电管、光电倍增管、光敏电阻、光电池、光敏二极管及光敏晶体管等，它们的作用是检测照射其上的光通量。选用何种形式的光电转换元器件取决于被测参数所需的灵敏度、响应速度、光源的特性及测量环境和条件等。

9.2 光电效应与光电器件※

光子是具有能量的粒子，每个光子的能量可表示为

式中

• \(h\)  —— 普朗克常数（ \(h = 6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\) ）；
• \(\omega\)  —— 光的振动频率。

根据爱因斯坦假设：一个光子的能量只给一个电子。因此，如果一个电子要从物体中逸出，必须使光子能量  \(E\)  大于表面逸出功  \(A_{0}\) ，这时，逸出表面的电子具有的动能可用光电效应方程表示为

式中

• \(m\)  —— 电子的质量；
• \(v\)  —— 电子逸出的初始速度。

根据光电效应方程，当光照射在某些物体上时，光能量作用于被测物体而释放出电子，即物体吸收具有一定能量的光子后所产生的电效应，这就是光电效应。光电效应中所释放出的电子叫光电子，能产生光电效应的敏感材料称作光电材料。光电效应一般分为外光电效应和内光电效应两大类。根据光电效应可以做出相应的光电转换元器件，简称光电器件或光敏器件，它是构成光电式传感器的主要部件。

9.2.1外光电效应※

当光照射到金属或金属氧化物构成的光电材料上时, 光子的能量传给光电材料表面的电子，如果入射到表面的光能使电子获得足够的能量，电子会克服正离子对它的吸引力，脱离材料表面而进入外界空间，这种现象称为外光电效应。即外光电效应是在光线作用下，电子逸出物体表面的现象。

根据外光电效应制作的光电器件有光电管和光电倍增管。

9.2.2 内光电效应※

内光电效应是指物体受到光照后所产生的光电子只在物体内部运动，而不会逸出物体的现象。内光电效应多发生于半导体内，可分为因光照引起半导体电阻率变化的光电导效应和因光照产生电动势的光生伏特效应两种。光电导效应是指物体在入射光能量的激发下，其内部产生光生载流子（电子-空穴对），使物体中载流子数量显著增加而电阻减小的现象；这种效应在大多数半导体和绝缘体中都存在，但金属因电子能态不同，不会产生光电导效应。光生伏特效应是指光照在半导体中激发出的光电子和空穴在空间分开而产生电位差的现象，是将光能变为电能的一种效应。光照在半导体PN结或金属-半导体接触面上时，在PN结或金属-半导体接触面的两侧会产生光生电动势，这是因为PN结或金属-半导体接触面因材料不同质或不均匀而存在内建电场，半导体受光照激发产生的电子或空穴会在内建电场的作用下向相反方向移动和积聚，从而产生电位差。

基于光电导效应的光电器件有光敏电阻；基于光生伏特效应的光电器件典型的有光电池；此外，光敏二极管、光敏晶体管也是基于光生伏特效应的光电器件。

9.3 CCD图像传感器※

9.4 光纤传感器※

在实际应用中发现，光纤受到外界环境因素（如温度、压力、电场、磁场等）的影响时，其传输的光波特征参量（如光强、相位、频率、偏振态等）将发生变化。如果能测量出光波特征参量的变化，就可以知道导致这些光波特征参量变化的温度、压力、电场、磁场等物理量的大小，于是出现了光纤传感技术和光纤传感器。

光纤传感器与传统的各类传感器相比有一系列独特的优点，如频带宽、动态范围大、灵敏度高、抗电磁干扰、耐高温、耐腐蚀、电绝缘性好、防爆、光路可绕曲、结构简单、体积小、重量轻、耗电少、易于实现远距离测量等。光纤传感器可以测量的非电量有70多种，如位移、压力、温度、流量、速度、加速度、振动、应变、磁场、电场、电压、电流、化学量、生物医学量等。

温度、压力、电场、磁场、振动等外界因素作用于光纤时，会引起光纤中传输的光波特征参量（振幅、相位、频率、偏振态等）发生变化，只要测出这些参量随外界因素的变化关系，就可以确定对应物理量的变化大小，这就是光纤传感器的基本工作原理。

要构成光纤传感器，除光导纤维外，还必须有光源和光探测器。

9.4.1 光纤的结构※

9.4.2 光纤的传光原理※

9.4.3 光导纤维的主要参数※

• 数值孔径
• 光纤模式
• 传播损耗
  • 材料吸收损耗（因材料密度及浓度不均引起）
  • 散射损耗（因光纤拉制时粗细不均匀引起）
  • 光波导弯曲损耗（因光纤在使用中可能发生弯曲引起）

9.5 光电式编码器※

9.6 计量光栅※

10 辐射与波式传感器※

10.1 红外传感器※

10.2 微波传感器※

10.3 压电式超声波传感器※

时差法测流速※

采用时差法测流量的超声波传感器称为时差式超声波流量计，目前应用最为广泛。当A为发射换能器，B为接收换能器时，超声波为顺流方向传播，传播速度为  \(c + v\cos \theta\) ，所以顺流传播时间  \(t_1\)  为

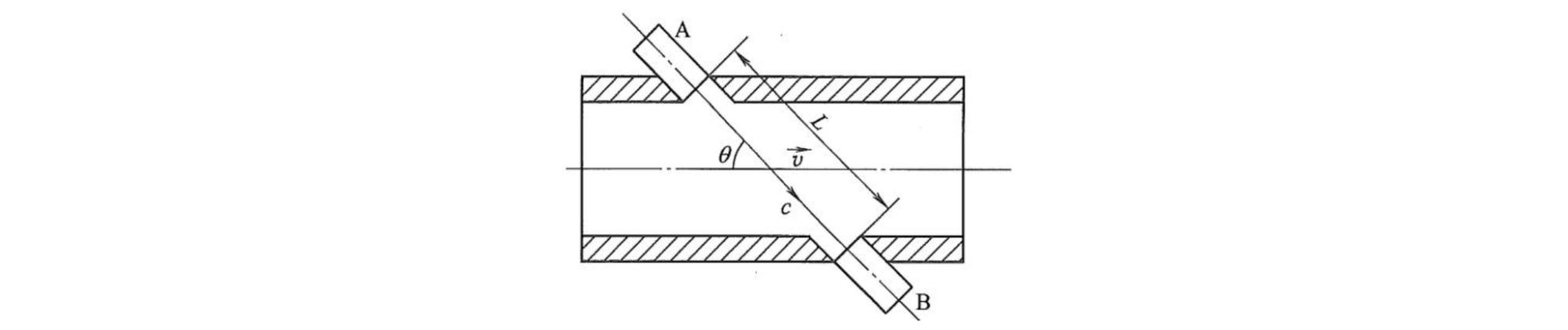
当B为发射换能器，A为接收换能器时，超声波为逆流方向传播，传播速度为  \(c - v\cos \theta\)  ，所以逆流传播时间  \(t_2\)  为

因此超声波顺、逆流传播时间差为

一般来说，超声波在流体中的传播速度远大于流体的流速，即  \(c >> v\)  ，所以式（10-26）可近似为

因此被测流体的平均流速为

测得流体流速  \(v\)  后，再根据管道流体的截面积，即可求得被测流体的流量。

超声波探伤※

• 穿透法探伤：
  • 穿透法探伤是根据超声波穿透工件后能量的变化情况来判断工件内部质量
• 反射法探伤：
  • 反射法探伤是根据超声波在工件中反射情况的不同来探测工件内部是否有缺陷。
  • 它又分为一次脉冲反射法和多次脉冲反射法两种。

超声波指纹识别※